-
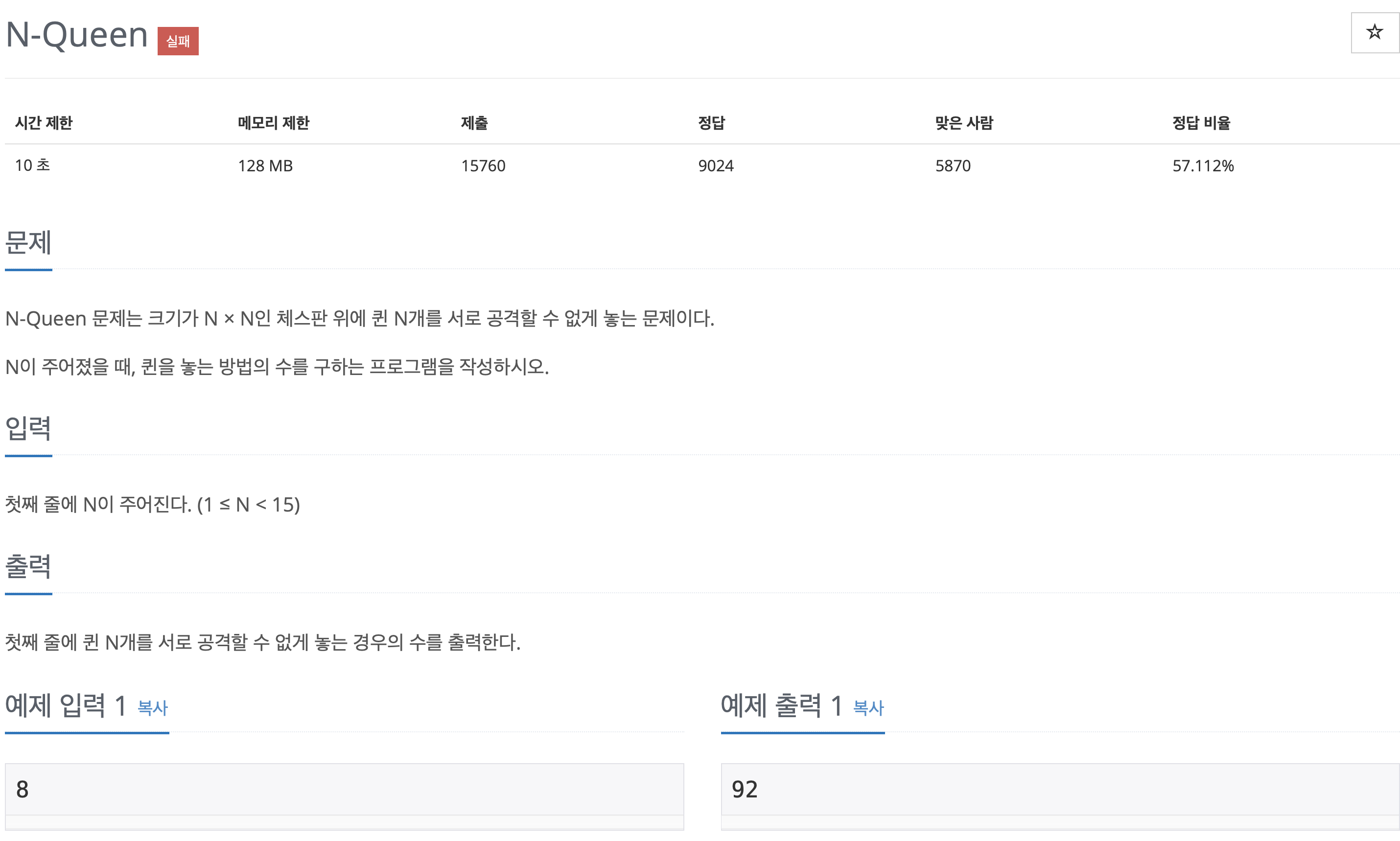
[백준 9663] N-Queen알고리즘/Brute Force 2019. 12. 25. 22:01
Type : 백 트랙킹
Queen 이란?
- 상,하, 좌, 우 대각선으로 모두 움직일 수 있는 체스의 말을 뜻한다.
나의 접근
공격 범위를 1부터 n까지 증가 시키며 첫 Queen의 위치를 (y, x)로 둔다.
공격 범위 1 첫 Queen의 위치 : (0, 0) 첫 Queen의 위치 : (0, 1) 첫 Queen의 위치 : (0, 2) ... 공격 범위 2 첫 Queen의 위치 : (0, 0) 첫 Queen의 위치 : (0, 1) 첫 Queen의 위치 : (0, 2) ... ...주어진 위치와 공격범위를 대상으로 n개의 queen을 놓을 수 있는지 검사한다.
- 주어진 위치에는 반드시 Queen을 놓는다.
- 공격 거리를 점차 증가 시킨다.
- y, x가 어느것과도 겹치지 않으면 Queen을 놓는다.
- Queen을 놓은 횟수가 n과 일치하는지 반환한다.
table[y][x] = 1; x+=1; int cnt = 1; while(y<n){ while(x<n){ if(!overlap(y, x, dist)){ table[y][x] = 1; cnt++; if(cnt==n) return true; } x++; } x = 0; y++; } return false;- 겹침 여부 검사
- 1부터 주어진 값까지 공격범위를 넓혀 나간다.
- 상,하, 좌, 우, 상좌, 하좌, 상우, 하우 순으로 탐색을 실시한다.
- 현재 위치 + (방향 * 공격범위) 로 탐색 지점을 구한다.
- 탐색 지점에 Queen이 놓여져 있다면 true를 반환 한다.
- 모든 탐색이 끝나도록 Queen이 발견되지 않는다면 false를 반환 한다.
int dy[8] {0, 0, -1, 1, -1, -1, 1, 1}; int dx[8] {-1, 1, 0, 0, -1, 1, -1, 1}; for(int d = 1; d <= dist ; d++){ for(int i = 0 ; i < 8 ; i++){ int ny = y + (dy[i] * d); int nx = x + (dx[i] * d); if(0<=ny && ny < n && 0 <= nx && nx < n){ if(table[ny][nx] == 1) return true; } } } return false;결과 : 틀렸습니다
모범답안 접근 및 풀이
백트랙킹 이란?
- 어떤 노드의 유망성을 점검 한 후, 유망하지 않으면 노드의 부노 노드로 퇴각 하여 다른 자손 노드를 검사 한다.
- 즉, 유망한 노드만 선택하여 깊이 우선 탐색을 실시한다.
모든 position(row, col)마다 탐색을 진행 하며 Queen을 놓을 수 있는지 여부를 검사한다.
만약 Queen을 놓을 수 있다면 다음열로 탐색을 진행 한다.for(int col = 0 ; col < n ; col++){ if(safe(row, col)){ table[row][col] = 1; addQueen(row+1); table[row][col] = 0; } }
safe 함수를 통해 다음 위치가 유망한지 여부를 검사한다.
부모 노드로 갈때는 놓은 Queen을 다시 되돌려 놓는다.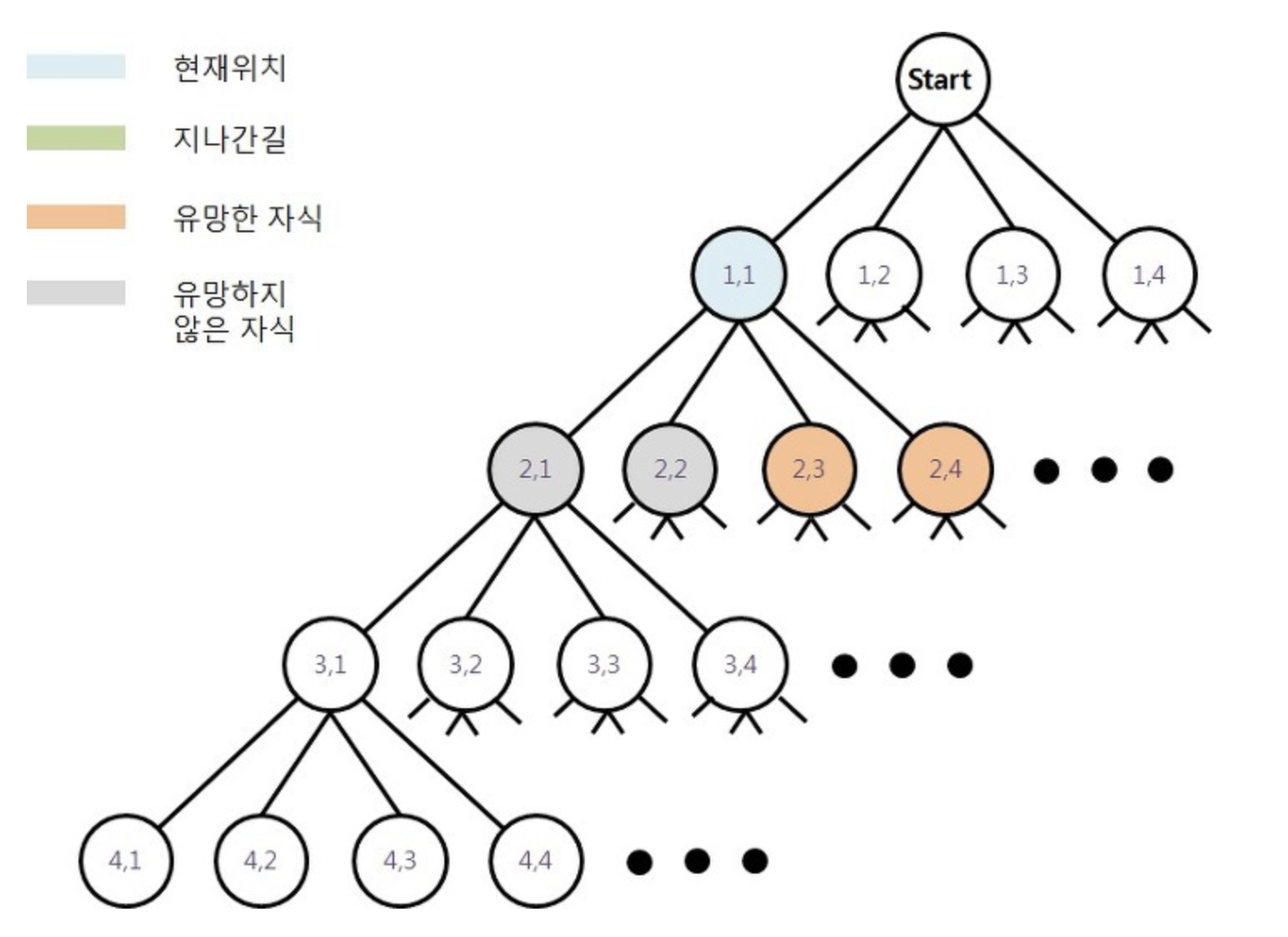
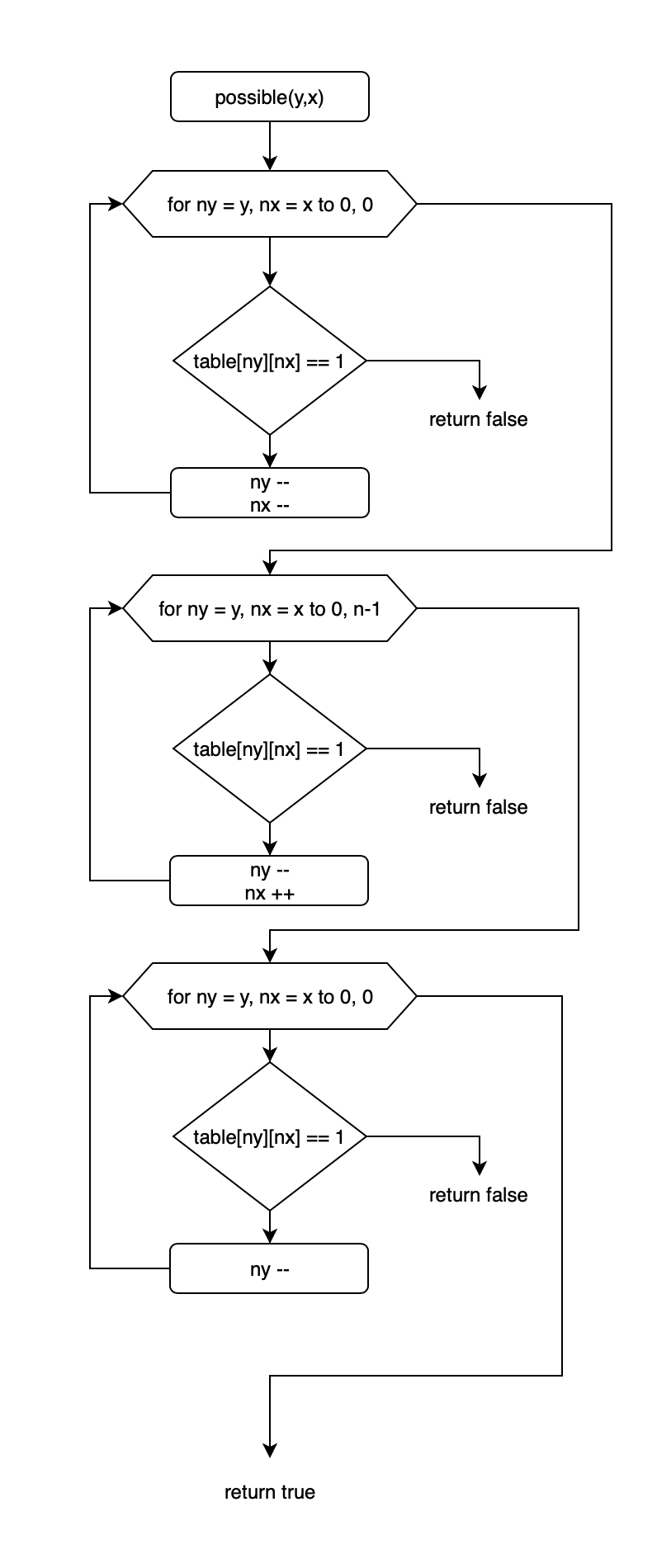
Safe 함수
- 주어진 위치를 기준으로 상, 좌상, 우상의 위치를 탐색한다.
- 탐색 과정중 Queen이 발견되면 false를 반환 한다.
//row-- (상) for(int row = y ; row >= 0 ; row--){ if(table[row][x] == 1) return false; } //row--col-- (좌상) for(int row = y, col = x ; row >= 0 && col >= 0; row--, col--){ if(table[row][col] == 1) return false; } //row--col++ (우상) for(int row = y, col = x ; row >= 0 && col < n; row--, col++){ if(table[row][col] == 1) return false; } return true; - row를 증가시키며 탐색하므로 하단부분은 탐색할 필요가 없다*
- 붙필요한 탐색을 줄여 시간을 줄일 수 있다*
플로우차트
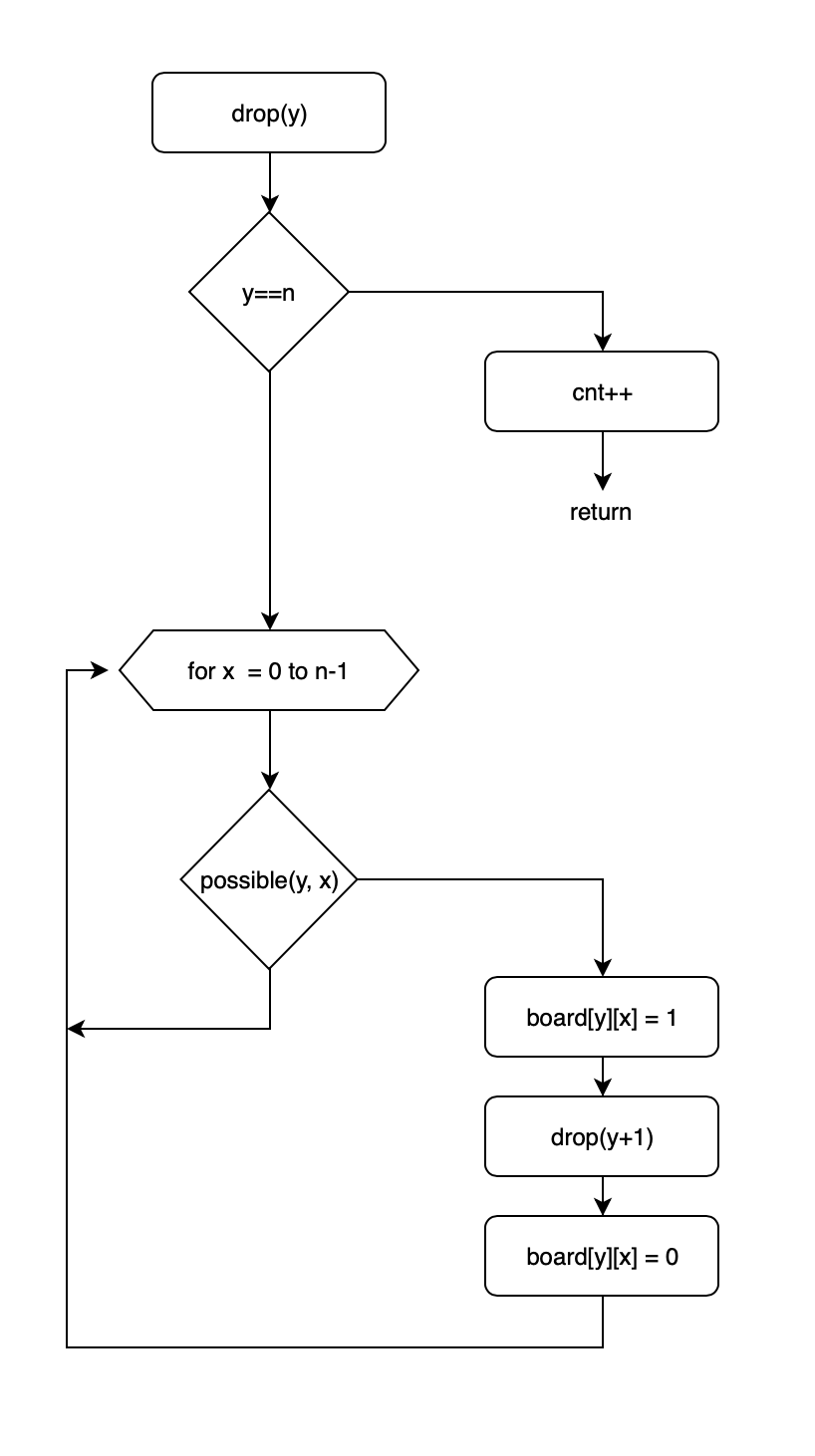
주요 코드
#include <iostream> #include <vector> #define MAX 15 using namespace std; int board[MAX][MAX]; int n, num; bool possible(int y, int x){ for(int ny = y, nx = x; ny>=0&&nx>=0 ; ny--, nx--){ if(board[ny][nx] == 1) return false; } for(int ny = y, nx = x; ny>=0&&nx<n ; ny--, nx++){ if(board[ny][nx] == 1) return false; } for(int ny = y, nx = x; ny>=0&&nx>=0 ; ny--){ if(board[ny][nx] == 1) return false; } return true; } void drop(int y){ if(y == n){ num+=1; return; } for(int x = 0; x < n ; x++){ if(possible(y, x)){ board[y][x] = 1; drop(y+1); board[y][x] = 0; } } } int main(int argc, const char * argv[]) { num = 0; cin>>n; //board[0][0] = 1; drop(0); cout<<num<<endl; return 0; }깨달은 점
- 같은 내용이라고 함수 호출을 하지 않는 것이 빠르다
- 동일한 내용의 변수를 계속 선언하고 초기화 하는데 시간이 소요됨 (전역 변수 사용)
- 상수 값을 사용 하는 것이 메모리내의 값 참조 보다 훨씬 빠름
'알고리즘 > Brute Force' 카테고리의 다른 글
[백준 6064] 카잉달력 (0) 2019.12.26 [백준 1248] 맞춰봐 (0) 2019.12.26 [백준 2580] 스도쿠 (0) 2019.12.25 [백준 1644] 소수의연속합 (0) 2019.12.16 [백준 1806]부분합 (0) 2019.12.16