-
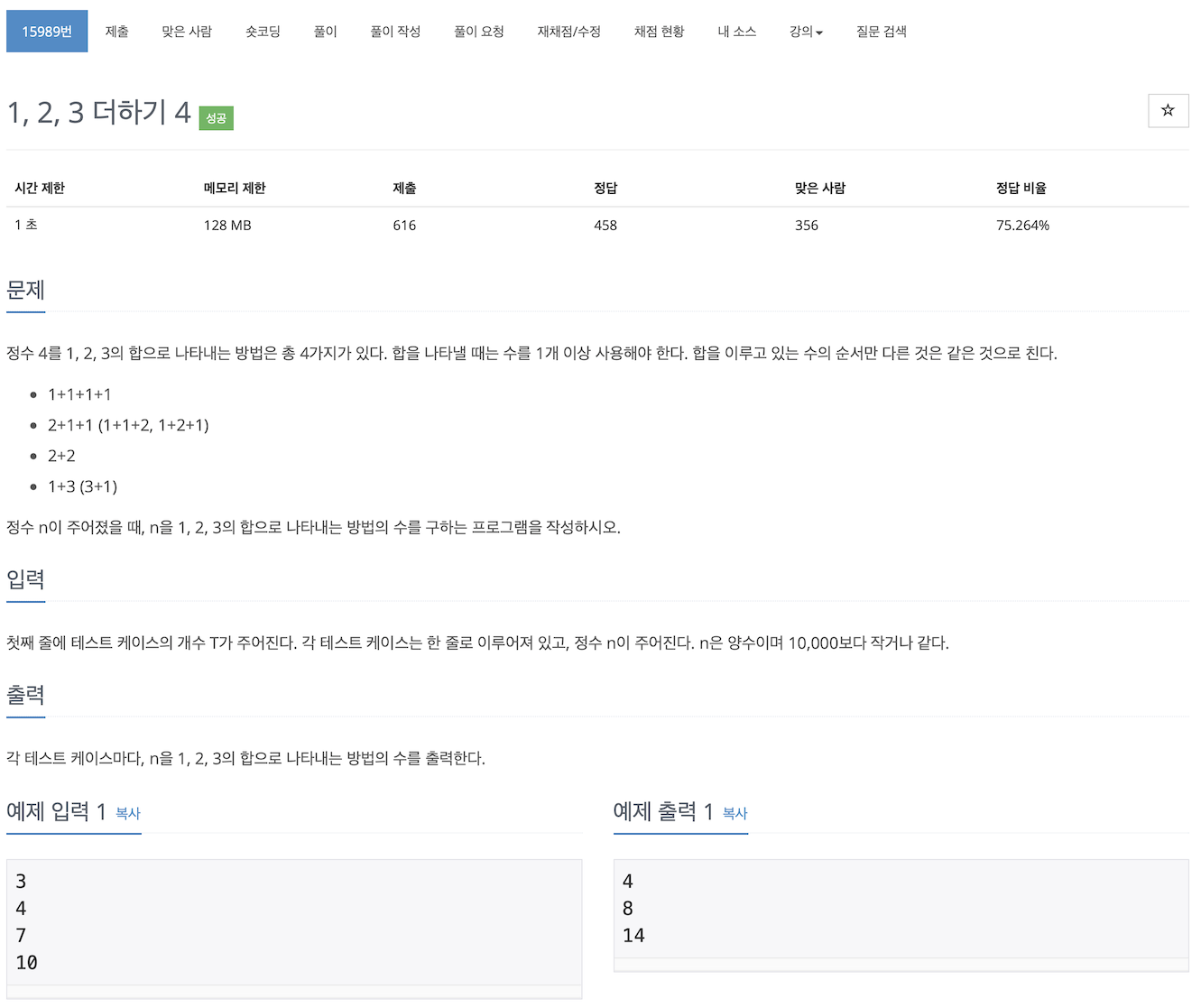
[백준 15989]1,2,3 더하기 4알고리즘/Dynamic Programming 2019. 12. 18. 09:57
Type : Dynamic Programming
접근
중복된 원소를 걸러내는 방법을 아는 것이 주요 포인트
중복을 방지하기 위헤 조건을 걸어야 한다
이 문제에선 맨 처음 숫자보다 작거나 큰수의 경우만 경우의 수로 합산한다
예를 들어 1 + 3 과 3 + 1 이 있을때 1 + 3 은 추가될 수 없다재귀 함수로 생각 해보기
int find(int num, vector<int> arr){ if(num == n){ if(arr.size() > 1 && arr[1] > arr[0]){ return false; } return true; } if(num > n){ return false; } ... }- 대략적인 재귀 함수의 탈출 조건을 생각하면 위와 같이 구성 할 수 있다.
- 하지만 재귀 함수를 통해 구현하면 시간 초과가 발생할 것이다
- 따라서 함수를 배열화 한 Dynamic Programming을 통해 문제에 접근한다.
- 함수의 배열화
1,2,3 더하기 3 문제 처럼 1부터 n 까지 숫자별로 경우의 수를 구해나간다
각 경우의 수는 아래와 같이 구한다- 1 부터 시작하는 경우
- 2 부터 시작하는 경우
- 3 부터 시작하는 경우
중복을 방지하기 위한 조건을 구해본다
- 만약 1 부터 시작 한다면 뒤에 올 수 있는 숫자는 1 밖에 없다
- 만약 2 부터 시작 한다면 뒤에 올 수 있는 숫자는 1 혹은 2 이다
- 만약 3 부터 시작 한다면 뒤에 올 수 있는 숫자는 1 혹은 2 혹은 3 이다
- 2차원 배열 활용
각 수마다 1, 2, 3 으로 시작되는 경우의 수를 저장 한다
3번의 설명처럼 시작되는 수와 중복을 방지하기 위한 조건을 지켜나가면서 배열을 채워나간다
dp[n][1] = dp[n-1][1]
dp[n][2] = dp[n-2][1] + dp[n-2][2]
dp[n][3] = dp[n-3][1] + dp[n-3][2] + dp[n-3][3]
n \ d 1 2 3 1 1 0 0 2 1 1 0 3 1 1 1 4 1 2 1 5 1 2 2 6 1 3 3 7 1 3 4
구현 코드
#include <iostream> #define MAX 10002 using namespace std; int dp[MAX][3]; void build(){ dp[1][0] = 1; dp[1][1] = dp[1][2] = 0; dp[2][0] = dp[2][1] = 1; dp[2][2] = 0; dp[3][0] = dp[3][1] = dp[3][2] = 1; for(int i = 4 ; i < MAX ; i++){ for(int j = 0 ; j < 3 ; j++){ for(int k = 0 ; k <= j ; k++){ dp[i][j] += dp[i-j-1][k]; } } } } int main(int argc, const char * argv[]) { build(); int t, n; cin>>t; for(int i = 0 ; i < t; i++){ cin>>n; cout<<dp[n][0] + dp[n][1] + dp[n][2]<<endl; } return 0; }깨달은 점
- 뒤에 올수 있는 숫자에 제한을 걸어 중복을 방지할 수 있다
- 2차원 배열을 통해 재귀함수를 배열화 할 수 있다
'알고리즘 > Dynamic Programming' 카테고리의 다른 글
백준_2163 초콜릿 자르기 (0) 2020.01.29 [백준 15988]123 더하기 3 (0) 2019.12.16 [백준 12101]123 더하기2 (0) 2019.12.16 [백준 9095]123 더하기 (0) 2019.12.13 [백준 2294] 동전 2 (0) 2019.12.10